EJERCICIOS RESUELTOS ELECTRÓNICA DIGITAL

En esta entrada de Apuntes de Ingeniería Gratis os dejamos dos ejercicios resueltos de electrónica digital.

El primero de ellos, tenemos un circuito RL simple

Nos piden hallar la corriente del circuito, tanto en su régimen permanente como su evolución transitoria, teniendo en cuenta que la corriente es nula en t=0

APUNTES DE INGENIERÍA GRATIS: Ejercicio resuelto Electrónica Digital 1

En el segundo, tenemos otro circuito 

Igual que el anterior, pero en este caso la corriente tiene caracter senoidal. Nos piden hayar la expresión de la corriente que pasa por el circuito.

APUNTES DE INGENIERÍA GRATIS: Ejercicio Resuelto de Electrónica Digital 2

CONFORMACIÓN POR DEFORMACIÓN PLÁSTICA (Tercera parte)

En esta Tercera Parte de Apuntes de Ingeniería Gratis sobre Conformación por Deformación Plástica hablaremos de la Deformación Plástica de los Materiales Policristalinos, para después centrarnos en la Temperatura de los Procesos de Conformación por Deformación Plástica, donde distinguiremos los procesos de trabajo en frío y los procesos de trabajo en caliente, así como la temperatura de Recristalización.

SEGUNDA PARTE: Conformación por Deformación Plástica (Apuntes de Ingeniería Gratis)

Deformación Plástica de los Material Policristalinos.

Cuando un metal policristalino (cualquier metal usado en la ingeniería), que dispone de granos equiaxiales y uniformes se somete a una deformación plástica a temperatura ambiente (cuando trabajamos a temperaturas ambientes se le denomina trabajo en frío) los granos se deforman y se alargan. Tal y como se puede observar en la siguiente figura

Durante esta Deformación Plástica, los límites de los granos permanecen inalterables ya que la masa se mantiene contínua.

El metal deformado muestra mayor resistencia a seguir deformándose debido a la obstrucción de las dislocaciones con los límites de los granos. Tal y como vimos en entradas anteriores de este blog de Apuntes de Ingeniería Gratis, denominándosele a este fenómeno con el término de acritud.

A mayor esfuerzo exterior, mayor deformación y por tanto mayor grado de acritud.

Por otro lado este aumento de resistencia será mayor para metales con tamaño de grano más pequeño ya que tienen mayor área superficial de límites de grano mayor por unidad de volumen de metal y, por tanto mayor número de obstrucciones de las dislocaciones.

Influencia de la temperatura en el conformado plástico.

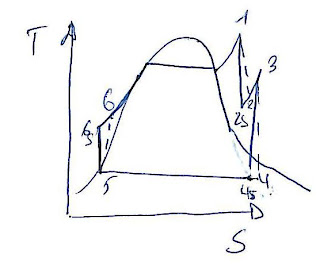
Si representamos en una gráfica el comportamiento de un metal del esfuerzo frente a la deformación durante la deformación plástica obtendremos la Curva de Fluencia.

Como se puede ver en la gráfica, tanto la resistencia, como el endurecimiento por deformación, se reducen a altas temperaturas. Por tanto, el trabajo en caliente produce un menor grado de acritud en el material, siendo más fácil su conformación plástica.

Cuando el metal se trabaja en caliente, las fuerzas requeridas para deformarlo son menores y las propiedades mecánicas cambian moderadamente. Cuando se trabaja en frío un metal, se requieren grandes fuerzas, pero la resistencia propia del material se incrementa constantemente.

El punto de temperatura que diferencia la zona de trabajo en caliente y la zona de trabajo en frío es la denominada Temperatura de Recristación. Que se define como la temperatura a la cual, un material deformado intensamente en frío recristaliza en una hora. Desarrollaremos este concepto de Temperatura de Recristalización mas abajo en esta misma entrada.

Para el acero, la recristalización se produce alrededor de 500 a 700 °C.

Pero hay que tener en cuenta que el aumento de la temperatura, tiene un límite ya que a mayores temperaturas, el material se hace más vulnerable, sufre alteraciones de composición si no está debidamente protegido. Y sobretodo hay que prestar especial atención a la presencia de oxígeno que puede producir óxido.

VENTAJAS DEL TRABAJO EN CALIENTE:

1. La porosidad en el metal provenientes de los procesos de fundición para obtener la material prima es eliminada.
2. Las impurezas en forma de inclusiones son destrozadas y distribuidas a través del metal.
3. Los granos gruesos o prismáticos son refinados
4. Las propiedades físicas generalmente se mejoran, debido al refinamiento del grano. Se desarrolla una gran homogeneidad en el metal.
5. Por todo lo visto anteriormente es fácil imaginar que la cantidad de energía para la conformación por deformación plástica de un material trabajando en caliente es mucho menor que la requerida si se trabaja en frío.

INCONVENIENTES DEL TRABAJO EN CALIENTE:

1. Debido a la alta temperatura, existe una rápida oxidación de la superficie, lo cual conlleva un pobre acabado superficial.
2. No pueden mantenerse tolerancias estrechas.
3. El equipo para trabajo en caliente y los costos de mantenimiento son altos.

TRABAJO EN FRÍO

• El producto obtenido con trabajo en f´rio no requiere de operaciones posteriores tales como enderezados o mecanizados.
• En el conformado en frío el material no experimenta un crecimiento del tamaño del grano por activación térmica
• Los granos se deforman por la acción de la deformación plástica, con lo que se consigue endurecimiento por acritud.

TEMPERATURA DE RECRISTALIZACIÓN

En esta misma entrada de Apuntes de Ingeniería Gratis habíamos hablado de la temperatura de recristalización como la temperatura que servía de guía para identificar una temperatura de trabajo en caliente y otra temperatura de trabajo en frío.

El proceso de recristalilzación consiste en la formación de nuevos granos en el metal policristalino a partir de granos ya existentes. Siempre y cuando estos granos existentes hayan sido previamente deformados en frío.

Este proceso consiste en:

1. Se calienta un material, previamente deformado en frío, hasta una temperatura no demasiado elevada durante un tiempo corto.
2. Se provoca un cierto ablandamiento del material sin modificación de su estructura interna.
3. Si el material está un tiempo suficiente a esta temperatura, los granos, que se habían deformado alargándose, tienden a recuperar la forma equiaxial de equilibrio y a su vez la agitación térmica provoca un incremento de su tamaño.

Esta temperatura de recristalización suele estar en torno a 0.5 Tf (temperatura de fusión), en esta temperatura los átomos se mueven y se difunden para formar núcleos nuevos. El material tiene suficiente energía interna para producir esta recristalización ya que previamente ha absorbido energía en la deformación en frío.

Esta temperatura de recristalización dependerá de los siguientes factores:

• Cantidad de trabajo: cuanto mayor es el grado de deformación menor es la temperatura de recristalización ya que, a mayor cantidad de trabajo aplicado mayor es la cantidad de energía acumulada internamente.
• Tamaño de grano antes de la deformación plástica: a menor tamaño de grano menor será la temperatura de recristalización, porque la estructura del grano pequeña tiene mayor cantidad de límites de grano, y a menor tamaño es más difícil deformar el grano.
• Temperatura: a menor temperatura de deformación plástica menor será la temperatura de recristalización.
• Tiempo de calentamiento para lograr la recristalización: a mayor tiempo menor será la temperatura de recristalización.
• Impurezas: cuando las impurezas son insolubles no afecta la temperatura de recristalización, pero si lo son si afecta, generalmente elevándolas.

EJERCICIO RESUELTO DE CINEMÁTICA Y DINÁMICA DE MÁQUINAS: Cálculo puerta trasera de una furgoneta

En este Ejercicio resuelto de Cinemática y Dinámica de Máquinas, de Apuntes de Ingeniería Gratis, podemos ver como a partir de un diseño inicial o un croquis, gracias a los cálculos de Cinemática y Dinámica se calculan esfuerzos, velocidades de los elementos del mecanismo, idoneidad o no del diseño...

En el ejercicio se nos dá el siguiente croquis como dato de partida:

En el que podemos ver dimensiones, número de eslabones del mecanismo y posición inicial. A partir de este croquis nos piden:

1) Dibujar un esquema cinemático del mecanismo y determinar la posición de cada uno de los eslabones cuando el portón trasero está en posición horizontal.

Este es el primer paso que siempre tenemos que dar en cualquier ejercicio de Cinemática y Dinámica de Máquinas, construir el esquema cinemático o cinema de velocidades.

En este caso es muy sencillo, únicamente hay que calcular un ángulo que no nos lo dan en el esquema inicial, para lo cual utilizaremos el teorema del coseno.

DESCARGAR EL EJERCICIO COMPLETO

2) Determinar el vector velocidad lineal del punto B extremo del portón cuando el vástago del cilindro se introduce a una velocidad constante de 1 mm/s, por el método de velocidades relativas.

Aplicar el método de las velocidades relativas en este problema es sencillo. Descárgate en esta entrada de Apuntes de Ingeniería Gratis el ejercicio completo con todos los pasos.

DESCARGAR EL EJERCICIO COMPLETO


3) Determinar el vector aceleración lineal del punto B.

El método empleado para calcular el vector aceleración del punto B es similar al empleado en el apartado anterior.

Lógicamente, las fórmulas empleadas en ambos apartados son distintas, pero el camino para ir de un eslabón a otro es el mismo.

DESCARGAR EL EJERCICIO COMPLETO

4) Determinar el vector velocidad lineal del punto B por el método del C.I.R., cuando el vástago del cilindro se introduce a una velocidad conocida.

Para calcular la velocidad del punto B mediante el método de los centros instantáneos de rotación, hay que establecer a que eslabón pertenece la velocidad conocida. En este caso la velocidad conocida será la velocidad del vástago que ya hemos demostrado que esta velocidad es igual a la velocidad del punto O3, con lo cual la velocidad conocida pertenece al eslabón 3.

Por otro lado la velocidad que queremos determinar, punto B, pertenece al eslabón 2.

Por  tanto hay que encontrar los centros instantáneos de la terna (1, 2, y 3), es decir (1,2), (1,3) y (2,3). Estos centros lo encontramos en la siguiente figura.

DESCARGAR EL EJERCICIO COMPLETO

5) Plantear la/s ecuación/es de cierre necesarias para encontrar las expresiones analíticas de la incógnitas cinemáticas.

Como el número de eslabones es 4, el número de ecuaciones de cierre es 1. La ecuación de cierre viene reflejada en la figura siguiente:

DESCARGAR EL EJERCICIO COMPLETO

6) Calcular la fuerza, Feq, que debe ejercer el cilindro del sistema elevador, en la dirección del vástago, para que soporte el peso P del portón en la posición indicada.

DESCARGAR EL EJERCICIO COMPLETO

APUNTES DE ÁLGEBRA. TRANSPARENCIAS DE CLASE.

Siguiendo con la finalidad del blog, la de recoger Apuntes de Ingeniería Gratis, en esta entrada os dejo unas transparencias de clase de la asignatura de Álgebra.

Estos Apuntes de Álgebra aunque son esquemáticos, aparecen todos los conceptos mas comunes de la asignatura.

Corresponden a la carrera de Ingeniería Industrial.

Son muy útiles para el último repaso antes de entrar al examen.

APUNTES DE INGENIERÍA GRATIS: Álgebra, transparencias de clase.

EJERCICIO RESUELTO MECÁNICA DE FLUIDOS (Tobera convergente-divergente)

En esta entrada os dejo un Ejercicio Resuelto de Mecánica de Fluidos de una tobera convergente-divergente de la asignatura de Mecánica de Fluidos II de Ingeniería Industrial.

En este ejercicio resuelto, de Apuntes de Ingeniería Gratis, tenemos una tobera convergente-divergente conectada a un depósito, que contiene 1 m3 de aire a una presión de 6·105 N/m2, con aire exterior a presión ambiente de 105 N/m2.

Se pide:
a) Deducir la evolución temporal de la cantidad de masa que permanece en el depósito hasta que deja de producirse bloqueo sónico. ¿Cuánto masa se conserva en el depósito en ese instante?.
b) Calcular la presión en el depósito cuando se alcanza por primera vez flujo totalmente isentrópico tanto dentro como fuera de la tobera (paso de onda de expansión a onda de choque oblicua).

DESCARGA: Ejercicio Resuelto Mecánica de Fluidos (Tobera convergente-divergente)

CUESTIONES RESUELTAS DE ELASTICIDAD Y RESISTENCIA DE MATERIALES

A menudo en los exámenes de Elasticidad y Resistencia de Materiales aparecen pequeñas cuestiones de caracter teórico de esta asignatura.

En los exámenes de Ingeniería el valor de las Cuestiones es pequeño comparado con el valor de los problemas. Pero si aseguráis algunas cuestiones en el examen estaréis mucho mas cerca del aprobado.

En esta entrada de Apuntes de Ingeniería Gratis, os dejo dos archivos con Cuestiones resueltas.

DESCARGAR: Cuestiones Resueltas de Elasticidad y Resistencia de Materiales 1

DESCARGAR: Cuestiones Resueltas de Elasticidad y Resistencia de Materiales 2

EXAMEN RESUELTO DE CINEMÁTICA Y DINÁMICA DE MÁQUINAS.

Hoy en nuestro blog de Apuntes de Ingeniería Gratis, publicamos un examen resuelto para el estudio de Cinemática y Dinámica de Máquinas de un mecanismo de seis eslabones.

En este problema de Cinemática y Dinámica de Máquinas nos piden:

1. Determinar la posición de cada uno de los eslabones del mecanismo.
2. Determinar el vector de velocidad lineal del punto C6, por el método de velocidades relativas. Sabiendo que la velocidad angular.
3. Determinar la aceleración angular del eslabón 4 sabiendo la aceleración de uno de ellos.
4. Determinar el vector de velocidad lineal del punto C por método de los C.I.R.
5.  Encontrar las expresiones analíticas de las incógnitas cinemáticas de posición por medio de la ecuación de cierre de Raven. En un dibujo indicar todas las variables que aparecen en la ecuación.
6. Calcular el valor del par equilibrante en el eslabón 2, planteando el equilibrio de cada eslabón.

DESCARGAR: Examen Resuelto de Cinemática y Dinámica de Maquinas.

TEOREMA DEL TRABAJO MÍNIMO. EJEMPLO RESUELTO.

En esta entrada publicamos un ejemplo resuelto del Teorema del Trabajo Mínimo para el Cálculo de Estructuras.

Tenemos la siguiente viga empotrada.

Como podemos ver en el diagrama se trata de una viga hiperestática, por tanto para su resolución utilizaremos el Teorema del Trabajo Mínimo.

Para poder utilizar el Teorema del Trabajo Mínimo tenemos que hacer antes el diagrama de momentos y flectores para toda la viga. Por tanto el proceso a seguir es:

1. DSL
2. Equilibrio de las secciones para determinar el diagrama de momentos, M(x)
3. Encontrar la Energía Interna de Deformación, U.
4. Aplicar el Teorema del Trabajo Mínimo.
5. Resolver el valor de la incógnita.
6. Determinar de forma numérica, las reacciones y los diagramas de la viga.

SOLUCIÓN.-

1) DSL.- Se trata de una viga hiperestática de grado 1.

Se ponen todas las incógnitas en función de una única incógnita, que en este caso hemos elegido que sea la Ax.

2) Determinar los diagramas de Momentos Flectores, M(x).-Se va calculando el equilibrio de las secciones desde A hasta B, de manera que los valores de las reacciones en el punto B no intervienen en la resolución. Todo quedará en función de R que es nuestra incógnita.

Los diagramas de momentos de la viga vienen determinados por dos tramos:

3), 4) y 5) Aplicación del Teorema del Trabajo Mínimo.-

Calculamos la integral

El valor de R es

R=(5/16)P

6) Determinar de forma numérica, las reacciones y los diagramas de la viga.

Reacciones:

Diagramas

CONFORMACIÓN POR DEFORMACIÓN PLÁSTICA (Segunda parte)

Seguimos publicando Apuntes de Ingeniería Gratis sobre Conformación por Deformación Plástica. En esta segunda parte hablaremos de la deformación de los cristales metálicos, de cómo una imperfección cristalina crea un sistema de deslizamiento y favorece la conformación por deformación plástica. Terminaremos esta entrada hablando del concepto de grano y frontera de grano.

PRIMERA PARTE Conformación por Deformación Plástica (Apuntes de Ingeniería Gratis)

La deformación en cristales metálicos

Cuando un material cristalino se somete a fuerzas de deformación exteriores, primero el cristal se deforma de modo elástico. Esto ocurre ya que la red cristalina se va alargando sin cambios en la posición de los átomos en la red. Por tanto si se elimina la fuerza exterior, la estructura vuelve a su posición original.

La deformación plástica sólo ocurre cuando el esfuerzo exterior supera el límite elástico del material

Ciertas imperfecciones de la red cristalina, como son las dislocaciones, tienen un papel muy importante para facilitar el deslizamiento en los metales.

Cuando una estructura de red que contiene una dislocación de borde se somete a una fuerza cortante, el material se deforma con mucha mayor facilidad que si se tratara de una estructura perfecta.

A la combinación de un plano de deslizamiento y su dirección de deslizamiento se le conoce como sistema de deslizamiento. 

Granos y límites de grano.

Casi todos los metales que se utilizan en el industria constan de muchos cristales individuales orientados al azar (granos).

En la fabricación de la materia prima, cuando el metal fundido comienza a solidificar, los cristales empiezan a formarse independientemente unos de otros en varios lugares dentro de la masa líquida, con orientaciones al azar y sin relación unas con otras.

El número y tamaños de los granos desarrollados en una unidad de volumen del metal dependen de la velocidad a la que tiene lugar la nucleación. El número de lugares diferentes en los que se comienzan a formar los cristales individuales y la velocidad a la que éstos crecen, influyen en el tamaño medio de los granos desarrollados. Si la velocidad de nucleación es alta, el número de granos en una unidad de volumen del metal será grande y, por lo tanto, el tamaño de grano será pequeño, y viceversa.  Generalmente, el enfriamiento rápido produce granos más pequeños, mientras que el lento produce granos más grandes.

El tamaño de grano influye en las propiedades mecánicas de los metales. El tamaño grande del grano se asocia con resistencia, dureza y ductilidad bajas.

Si el grano del material es grande, si el material se somete a una laminación provocará una superficie de apariencia rugosa (efecto piel de naranja). 

Endurecimiento por deformación (acritud)

Durante la deformación plástica, las dislocaciones pueden obstruirse unas con otras y verse impedido su desplazamiento por la aparición de barreras como límites de grano, impurezas, e inclusiones en el material.

A este aumento del endurecimiento del material cuando se somete a deformación plástica, se le denomina endurecimiento por resistencia a la deformación o acritud.

Cuanto mayor sea la deformación, mayor será el número de obstrucciones, y de ahí un aumento en la resistencia del metal.

El endurecimiento por deformación se emplea para aumentar la resistencia de los metales en los procesos de trabajo.

TERCERA PARTE: Conformación por Deformación Plástica (Apuntes de Ingeniería Gratis)

PROBLEMAS RESUELTOS DE TRANSFORMADORES

En esta entrada de Apuntes de Ingeniería Gratis os dejamos dos problemas resueltos de transformadores.

PROBLEMA 1.- 

Tenemos un transformador monofásico de 250 kVA, y una relación de transformación dada, que arroja lossiguientes resultados en los ensayos de vacío y cortocircuito.

Nos piden:

1º. El circuito equivalente eléctrico referido al primario y al secundario.

2º. El rendimiento a plena carga y con factor de potencia unitario.

3º. La caída de tensión en el transformador cuando alimenta una carga dada

4º. Corriente que circularía por el transformador si se produjera un cortocircuito en bornes del mismo.

DESCARGAR: Problema resuelto de transformadores





PROBLEMA 2.-

En una industria se dispone de los tres transformadores en serie para crear una red a 400V.

Nos piden:

1º Analizar cual es la combinación entre los distintos transformadores que proporciona la máxima potencia sin que ninguno trabaje sobrecargado.

2º Dibujar la conexión de este conjunto a las redes de A.T y B.T. Justificar en caso de que haya
cambios.

3º Calcular el circuito equivalente del mayor transformador del grupo, si se conocen los resultados de su ensayo en vacío.
4º Calcular la tensión del conjunto en el lado de baja.

DESCARGAR: Problema resuelto transformadores en serie

EXAMEN RESUELTO ELASTICIDAD Y RESISTENCIA DE MATERIALES II

En este Examen Resuelto de Elasticidad y Resistencia de Materiales nos dán la estructura, las reacciones y el tipo de sección. Nos piden diseñar la viga.

APUNTES DE INGENIERÍA GRATIS: Examen Resuelto Elasticidad y Resistencia de Materiales

EXAMEN RESUELTO ELASTICIDAD Y RESISTENCIA DE MATERIALES.

En esta entrada del blog Apuntes de Ingeniería Gratis, os dejo un Examen Resuelto de Elasticidad y Resistencia de Materiales de Ingeniería Industrial.

En este ejercicio dada la estructura siguiente:

Nos piden:

1.- Calcular los esfuerzos de cada elementos.
2.- Coeficiente de seguridad de cada barra para el estado dado.
3.- Flecha máxima en la viga AC.



DESCARGAR: Examen Resuelto Elasticidad y Resistencia de Materiales.

EJERCICIO RESUELTO DE CIRCUITOS. FÍSICA I.

En esta entrada tenéis un Ejercicio Resuelto de Circuitos de la asignatura Física I.

DESCARGAR: Ejercicio Resuelto de Circuitos.

EJERCICIOS RESUELTOS ELECTROMAGNETISMO. FÍSICA I.

En esta entrada os dejo dos ejercicios resueltos de electromagnetismo. Son los ejercicios que suelen caer siempre en los exámenes de Física I.

PROBLEMA 1.- Tenemos una distribución esférica de carga NO uniforme y nos piden calcular el campo eléctrico en todos los puntos y posteriormente el potencial eléctrico.

PROBLEMA 2.- Una espira conductora que se mueve dentro de un campo magnético variable. Calcular la intensidad de corriente eléctrica en diferentes situaciones.

Como ya he dicho, SON LOS QUE ENTRAN SIEMPRE EN LOS EXÁMENES.

DESCARGAR APUNTES DE INGENIERÍA GRATIS: Ejercicios resueltos de Electromagnetismo.

EJERCICIOS DE ELECTROTECNIA DE EXAMEN

En esta entrada de Apuntes de Ingeniería Gratis, os dejo dos ejercicios de electrotecnia de examen, aunque no están resueltos tienen su resultado al final de cada enunciado.

Tienen nivel de examen.

EJERCICIO 1.-

EJERCICIO 2.-

EJERCICIO RESUELTO TERMOTECNIA II. CICLO DE RANKINE CON RECALENTAMIENTO.

ENUNCIADO: En un ciclo de Rankine con recalentamiento intermedio, el vapor llega a la turbina de alta presión a 100 bar y 400ºC. El vapor se extrae a la presión de 40 bar y se recalienta hasta 400º C, expansionándose completamente en la turbina de baja presión. La presión en el condensador es de 0,07 bar. El rendimiento isoentrópico de cada una de las dos turbinas es del 80%. El trabajo en la bomba se considera despreciable. Calcular el rendimiento termodinámico del ciclo y la potencia de la instalaicón si el flujo de agua necesario es de 300.000 kg/hora.

SOLUCIÓN:

El ciclo de Rankine con recalentamiento intermedio tiene la siguiente gráfica.

A partir de la gráfica y de los datos que nos dá el enunciado podemos sacar:

Por tanto:

EJERCICIO RESUELTO DE TERMOTECNIA I

ENUNCIADO: En una turbina que funciona en régimen estacionario entra vapor a razón de 4.600 Kg/hora. La turbina desarrolla una potencia de 1.000 kW. A la entrada, la presión es de 60 bar, la temperatura 400º C y la velociad 10 m/seg. A la salida la presión es 0,1 bar, el título del vapor es 0,9 y la velocidad 50 m/seg. Calcular la velocidad de transferencia de calor entre la turbina y los alrededores, en kW.

SOLUCIÓN SEGÚN APUNTES DE INGENIERÍA GRATIS: Este tipo de problemas se hace utilizando la fórmula del balance de energía en un recinto de control.

CONFORMACIÓN POR DEFORMACIÓN PLÁSTICA (Primera parte)

Seguimos con la asignatura de Tecnología mecánica, en otras entradas del blog hemos visto las técnicas de fundición para obtener piezas a partir de metal fundido utilizando un molde de arena o un molde metálico.

Pasamos ahora a comentar los procesos de Conformación por Deformación Plástica que son procesos de fabricación, en los que mediante la acción de fuerzas exteriores se consigue modificar la geometría exterior del cuerpo de metal y variar las características mecánicas del mismo.

Lógicamente no todos los materiales son susceptibles de aplicarles estos procesos de Conformación por Deformación Plástica. Sólo son aptos los materiales con un amplio periodo plástico, o sea los que pueden experimentar una deformación permanente importante sin llegar a destruir sus enlaces moleculares (p. ej. el acero y algunos metales no férreos).

Por tanto, con un proceso de Conformación por Deformación Plástica conseguimos:

• Cambiar la geometría de la pieza.
• Incrementos de resistencia del material.
• Conformar piezas sin desperdiciar material.

1. ¿Cómo se comporta el material durante el proceso de Conformación por Deformación Plástica?

Para estudiar el comportamiento de un material ante la Deformación Plástica, utilizaremos la curva obtenida en un ensayo de tracción como la siguiente:

Curva característica de cada material Tensión-Deformación

En esta gráfica podemos distinguir varias zonas:

• OA.- La deformación es proporcional al esfuerzo. Zona de deformación elástica. Cuando cesan los esfuerzos exteriores el material recupera la forma. Lógicamente este rango de tensiones no nos interesa ya que no provocan deformaciones plásticas en el material.
• BC.- Esta es la zona que nos interesa. Los esfuerzos han provocado deformaciones, que una vez desaparecen, el material vuelve al punto E, con lo cual ha obtenido un incremento de tamaño OE (deformación plástica obtenida).

En esta zona el comportamiento del metal se define en la siguiente fórmula:

Donde K es el coeficiente de resistencia y n es el exponente de endurecimiento. En la siguiente tabla vemos valores de K y n para diferentes materiales:

Como regla general, los materiales metálicos se comportan según alguna de estas gráficas:

Cuando tenemos que diseñar una pieza a partir de un material, el único dato del que disponemos es el Límite elástico, que se obtiene a partir de ensayos de tracción. Por tanto nuestro estado de tensiones (generalmente tridimensional) debemos pasarlo a un estado monoaxial para poder comparar este estado monoaxial con el límite elástico dado.

Utilizaremos para ello, alguno de estos dos criterios:

1. Criterio de Tresca.-

Se utiliza para materiales dúctiles sometidos a estados de tensión en los que las tensiones tangenciales son relativamente grandes. Sólo se tomarán en cuenta dos de las tres direcciones principales.

     2. Criterio de Von-Misses.-

Según este criterio la aparición de deformación plástica viene de la energía de deformación que se le está trasmitiendo al material.

SEGUNDA PARTE CONFORMACIÓN POR DEFORMACIÓN PLÁSTICA (APUNTES DE INGENIERIA GRATIS)